One of the most common recurring problems in scaling your servers is deciding how many servers or how many cores you will need. Do I really need this many servers or is there something wrong with the way I implemented the server Architecture? Remember how flipkart.com failed to scale their servers. Horizontal vs Vertical vs Hybrid scaling is another important consideration. Is there a quantitative way you can make this decision? In this article I have tried to represent a mathematical model to fit into a web service request-response queuing mechanism which would answer these questions. I have used the Erlang–C model to compute the queue length and waiting times, which in turn can be used to fit the right number of servers required to serve a certain number of users. Before I pour a reservoir of details down your throat I will give you an insight into the various parameters that are involved. Note, I have curtailed all the details in arriving at the final results in order to keep the post short.
Input parameters
Mean request rate: λ: This is really dependent on the number of users and it very much follows a poisson distribution of request arrival (let’s say number of requests per hour).
Mean Service rate: µ: This is the number of service requests that your system can deliver. It really depends upon how long a service request takes. Imagine a typical search request might take O(nlogn )complexity and depending on the number of entries(n), you can compute the mean service time (this also has a certain O(n) time factor which might be directly dependent on the bandwidth costs which might be a major factor in some cases). A better way to measure this is by running a bunch of performance tests on your server to directly measure the mean response time and completely get rid of the bandwidth criteria.
Number of servers: S: For horizontal scaling. Let’s call S the horizontal scaling factor and µ the vertical scaling factor.
Out Parameters
Pn → Probability of n people waiting at any time
L → Expected wait queue Length in the same units as that of Λ
W → Expected wait time in the same units as the frequency of W = L / Λ
Distribution and the first expectation
We can arrive at the probability that no queue is maintained as:

Observant readers might have already smelled a bivariate Poisson distribution in: λ, µ and we can generalize it to n :
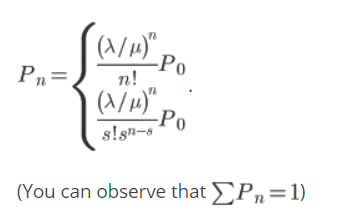
Now the expected waiting queue length can be derived from the first discrete expectation of n over the probability distribution.
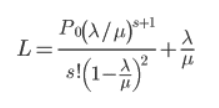
The computation of P0 is an O(nlogn) algorithm, on the other hand to fit the right number of servers to reduce the value of L down to a given required value would be a direct binary search In O(logn) time. Overall to find out the number of servers required to efficiently run your state system could be computed in O(nlog2 (n) ) time.
Applications:
- This can be applied on cloud based SAAS where server scalability is a very important issue.
- Proactive server scaling can be done if we know how long an individual http call can take to respond, depending on the complexity of the function returning the value in the back-end.
- Identifying performance bugs can be easy. We can easily identify performance issues or bottle necks rather than mindlessly increasing the number of servers or cores.
- Optimum number of cores per server vs number of servers required to achieve the most optimized performance scalability.
Assumptions:
- This really doesn’t count for new features that keep getting added and the new potential users that keep getting added. Over a period of time the mean request rate is always going to increase with time.
- Varying Bandwidths and network speeds and other infrastructure dependencies.
Improvements:
- Horizontal scaling factors, usually when you add two servers you always don’t get twice the performance, there is a certain performance cost just to maintain the new server as well. There are ways to measure state dependent performance scaling as well using Conway- Maxwell distribution.
- We can apply this to a finite state system where in there are a small number of users like in a typical enterprise environment.
- One can make a more quantified pricing model for deciding the server prices vs the number of server requests made.




